시험에 무조건 나오는 고차방정식 정복하기!
Contents
1. 사차방정식 풀이
2. 연립방정식이 한 쌍의 해를 가질 조건
3. 이차부등식 해가 없을 조건
4. 이차부등식 활용
5. 절댓값이 있는 연립부등식 풀이
수식이 깨지는 학생들은 다운로드하시면 됩니다.
※ 티스토리 블로그에서 소괄호가 깨지는 현상이 나타내서, 소괄호를 대괄호 [ ] 이렇게 대체했습니다.
[출제율 60%, 난이도 ☆☆★★]
문제1) 사차방정식 $ x^{4}+ax^{3}+ax^{2}+11x+b=0 $ 의 두 근이 -1, 1일 때, 나머지 두 근의 합을 구하시오.
정답) 11
해설)
step1) 두 근이 -1, 1이라고 했으므로, 대입하여 완전한 사차방정식을 구한다.
x=-1 대입 → 1 -a +a -11 +b =0 → b = 10
x=1 대입 → 1 +a +a +11 +b =0 → 2a = -22 → a=-11
$ x^{4}+ax^{3}+ax^{2}+11x+b=0 $ 이 $ x^{4}-11x^{3}-11x^{2}+11x+10=0 $ 으로 완전한 식이 되었다.
step2) $ x^{4}-11x^{3}-11x^{2}+11x+10=0 $ 을 조립제법을 사용해서 해를 다 구해보자.
근이 -1, 1이므로 $ (x+1)(x-1)(x^{2}-11x-10)=0 $
나머지 두 근은 $ x^{2}-11x-10=0 $ 에서 나온다.
두 근의 합은 11
[출제율 80%, 난이도 ☆☆★★]
문제2) 다음 연립방정식이 오직 한 쌍의 해를 가질 때, 실수 a의 값은?
$$ \left\{\begin{matrix}
x-2y=3 \\x^{2}+y^{2}=a
\end{matrix}\right. $$
정답) 9/5
해설)
step1) x= 3 +2y를 밑에 식에 대입
$ (3+2y)^{2}+y^{2}=a $
$ 9+12y+4y^{2}+y^{2}-a=0 $
$ 5y^{2}+12y+9-a=0 $
step2) 생각을 해보자. y에 대한 이차방정식인데, y의 값이 2개가 나오게 되면, x의 값도 2개가 나오게 되니, 해가 2쌍이 나오게 된다. 그러면 y의 값이 1개가 나오면 x의 값도 1개가 되므로, 한쌍이 된다.
y의 값이 한 쌍이 된다. → y에 대한 이차방정식이 중근을 가진다. → 판별식 $ b^{2}-4ac=0 $ 이다.
$ 5y^{2}+12y+9-a=0 $ 의 판별식이 0이다.
144 - 20 [9-a] =0
144 -180 +20a =0
20a = 36
a= 9/5
[출제율 70%, 난이도 ☆☆★★]
문제3) 이차부등식 $ ax^{2}+2x+a-4>0 $ 의 해가 없도록 실수 a의 값의 범위를 정하시오.
정답)
해설) 해가 무수히 많은지, 해가 없는지 판단하고, 그래프의 개형 6개를 파악한다.

step1) 이차함수가 0보다 큰 해가 하나도 없으려면, 그래프 6개 중 4, 5번 그래프가 되어야 한다.
위로 볼록인 함수이므로, a<0
step2) 판별식 $ b^{2}-4ac\leq 0 $ 이 되어야 한다.
$ 1-a(a-4)\leq 0 $
$ a^{2}-4a-1\geq 0 $
유리수로 인수분해가 되지 않아서, 실수의 범위로 확장을 해서 해를 구한다.
근의 공식을 쓰면 해는
$ \frac{4\pm \sqrt{16+4}}{2}=2\pm \sqrt{5} $
$ (a-2-\sqrt{5})(a-2+\sqrt{5})\geq 0 $ 범위가 큰큰 작작
$ a\geq 2+\sqrt{5}, a\leq 2-\sqrt{5} $
1번 단계에서 a<0 이라고 했으므로, 공통된 범위는
$ a\leq 2-\sqrt{5} $
[출제율 90%, 난이도 ☆☆☆★]
문제4) 아래 그림과 같이 한 변의 길이가 10m 인 정사각형 모양의 땅에 일정한 폭의 길을 만들었다. 꽃밭의 넓이가 64㎡ 이상이 되도록 할 때, 길의 폭의 범위를 정하시오.
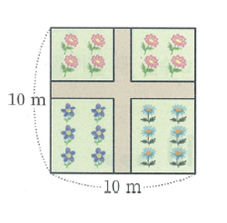
정답) 0m 초과 2m 이하
해설) 전체 넓이에서 길의 넓이를 뺄 생각을 한 학생도 좋고, 꽃밭 직사각형 4개를 다 붙여서 큰 직사각형으로 만들어도 괜찮다. 쌤은 후자를 사용하도록 하자.
step1) 길의 폭을 x라고 둔다. 그리고 꽃밭을 다 붙이면 큰 직사각형이 나오는데, 가로 × 세로로 넓이를 구해보자.
$ (10-x)(10-x)\geq 64 $
$ 100-20x+x^{2}\geq 64 $
$ x^{2}-20x+36\geq 0 $
$ (x-2)(x-18)\geq 0 $ 큰큰작작이다.
$ x\geq 18, x\leq 2 $
정사각형이 기존 10m 이였으니 18m 보다 큰 것은 말이 되지 않으며, $ x\leq 2 $
폭의 범위는
$ 0\leq x\leq 2 $
[출제율 70%, 난이도 ☆★★★]
문제5) 다음 연립부등식을 만족시키는 모든 정수 x의 값의 합을 구하시오.
$$ \left\{\begin{matrix}
\left|2x-1 \right|>1 \\ 2x^{2}-11x+5\leq 0
\end{matrix}\right. $$
정답) 14
해설)
step1) $ \left|2x-1 \right|>1 $ 을 잘 처리해 보자.
절댓값 2x-1 이 1이 되는 수를 찾는다.
+1, -1이 되고, 큰큰 작작이다.
2x-1 >1 , 2x-1 <-1
2x>2 , 2x <0
x>1, x <0
step2) $ 2x^{2}-11x+5\leq 0 $ 가 쉽게 인수분해가 된다.
$ (2x-1)(x-5)\leq 0 $
$ \frac{1}{2}\leq x\leq 5 $
연립부등식은 공통된 범위를 찾는다.
$ 1<x\leq 5 $
따라서 2, 3, 4, 5
- 끝 -
'수학 문제의 모든 것 > 고1 시험 적중 문제' 카테고리의 다른 글
| [고1 도형의 방정식 4회] 시험에 무조건 나오는 문제 [+개념복습] (1) | 2023.07.06 |
|---|---|
| [고1 고차방정식 4회] 시험에 무조건 나오는 문제 [+개념복습] (0) | 2023.07.04 |
| [고1 고차방정식 3회] 시험에 무조건 나오는 문제 [+개념복습] (1) | 2023.07.03 |
| [고1 평면좌표 복습 2회] 선분의 내분점, 외분점 + 빈출문제 정리하기! (0) | 2023.07.01 |
| [고1 도형의 방정식 3회] 시험에 무조건 나오는 문제 [+개념복습] (0) | 2023.06.22 |



