하이루~ 전 시간까지 부등식이 무엇인지, 부등호에 대해서 공부해 보고 부등식의 성질로 해를 구하는 간단한 방법까지 공부했다. 이번 시간은 본격적으로 부등식의 해를 구해보고, 부등식의 해를 수직선에 표현하는 방법 또한 공부해 보도록 하자. 내용이 많기 때문에, 이번 시간은 개념을 최대한 공부하면서 많이 나오는 대표 예제 문제들을 다뤄보도록 하자.
글씨가 깨지는 학생들을 위한 자료는 따로 올려놓을게!
Contents
1. 일차부등식이란?
2. 부등식의 해를 구하고, 수직선에 표현해 보기
3. 복잡한 일차부등식 풀이
1. 일차부등식이란?
일차부등식 : 부등식의 모든 항을 이항에서 정리했을 때, 일차식 꼴로 나오는 부등식을 일차부등식이라 한다.
예를 들면,
일차식 < 0, 일차식 > 0, 일차식 ≥ 0, 일차식 ≤ 0 형태가 되어야 한다.
예제1)
[1] x - 6 > 4x + 2
대충 봐도 식에 일차식과 상수밖에 없기 때문에, 일차식이 되지만, 꼼꼼한 학생들은 이항을 해보도록 한다. 앞으로 부등식의 해를 구하기 위해서는 이항과 부등식의 성질을 적용해서 해를 구해야 한다.
x - 4x -6 -2 > 0
-3x -8 > 0
좌변이 일차식이므로, 일차부등식이라 한다.
[2] $ x^{2}-6 > x^{2}-4x $
x의 제곱이라는 2차 항이 있으므로 이런 식은 이차부등식이라 한다.
[3] $ x^{2}-6 > x^{2}-4x $
얼핏 보면 이차부등식처럼 보이지만, 이항을 해보도록 한다. 우변의 식을 좌변으로 이항 하면,
$ x^{2}-x^{2}-6+4x > 0 $
이차항은 사라지게 된다.
-6 + 4x > 0 이 되므로, 이 식은 일차부등식이다.
2. 부등식의 해를 구하고, 수직선에 표현해 보기
해를 수직선에 표현하기 전에, 부등식의 해를 확실하게 구해보도록 한다.
중1에서 배웠던 방정식과 비슷하기 때문에, 복습이 잘 되어있으면 크게 어렵지 않다.
※주의할 점은 부등식의 양변에 음수를 곱하거나 나누면 부등호의 방향이 바뀐다는 것만 기억한다.
예제2) -7 -x > 9 -3x
step1) x가 있는 항은 좌변으로 모으고, 다른 항은 우변으로 모은다.
-x +3x > 9 +7
step2) 동류항끼리 계산한다.
2x > 16
step3) 부등식의 성질을 이용하여, 양 변에 2를 나눈다. 음수가 아니므로 부등호의 방향은 변화가 없다.
x > 8
step4) 부등식의 해를 수직선에 표현해 본다.

예제3) x -1 ≤ 3x -5
위의 단계와 같기 때문에, 빠르게 풀어본다.
step1)
x -3x ≤ -5 +1
-2x ≤ -4
step2) 우리의 목표는 x의 범위를 구하는 것이므로, 양변에 -2를 나눈다. 이때 음수를 나누게 되므로, 부등호의 방향이 바꾸는 것에 주의한다. 왕 중요하다!
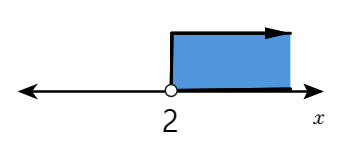
x ≥ 2
step3) 열심히 구한 해를 수직선에 표현해 본다.
3. 복잡한 일차부등식 풀이
[1] 괄호가 있는 일차부등식 : 분배법칙을 이용하여 괄호를 먼저 풀고 나서, 이항을 해서 동류항끼리 계산을 한다.
[2] 분수가 있는 일차부등식 : 분모의 최소공배수를 양변에 곱해서 계수를 정수로 만들어준다.
[3] 소수가 있는 일차부등식 : 양변에 10, 100, 1000과 같은 10의 거듭제곱을 곱하여 계수를 정수로 만든다.
- 끝 -
'수학 개념의 모든 것 > 중등수학' 카테고리의 다른 글
| [중2 기본] 3-5. 일차부등식 활용 완벽 마스터하기! (0) | 2023.03.17 |
|---|---|
| [중2 기본] 3-4. 일차부등식 활용 완벽 마스터하기! (1) | 2023.03.16 |
| [중2 기본] 3-2. 일차부등식 성질 완벽 마스터하기! (0) | 2023.03.14 |
| [중2 기본] 3-1. 일차부등식 완벽 마스터하기! (0) | 2023.03.13 |
| [중2 기본] 2-1. 지수법칙 완벽 마스터하기! (0) | 2023.03.08 |



