여러분 하이루~ 1단원이 마무리가 되고, 2단원 첫 번째 시간이야. 1단원과 2단원은 크게 연관되는 부분은 없어서, 1단원에서 조금 힘들었다 해도, 2단원 열심히 공부하면 되니깐, 새로운 마음으로 열심히 해 볼 수 있도록 하자.
우선 수학에서 배우는 수의 체계에 대해서 공부할 필요가 있어. 새로운 용어들이 많이 나오게 되니깐, 어느 정도 반복 학습은 필요하단다. 처음엔 어려울 거야...
Contents
1. 자연수와 정수
2. 유리수
3. 수직선 제대로 그리기
4. 양수와 음수
5. 중1 수의 체계 정리
1. 자연수와 정수
우선 쌤이 간단한 질문을 해볼게.
질문) 자연수가 뭐지?
답변) 1, 2, 3, 4 … 아닌가요?
정답이야. 자연수는 무언가를 셀 때, 자연스럽게 사용하는 수거든. 예를 들면, 지금 창문을 열고 밖에 지나가는 자동차의 수를 세어보자!라고 한다면, 1대, 2대, 3대 이렇게 말하겠지? 아마 1.2대, 2.7대 … 이렇게 말하는 학생들은 없을 거야.
자연수란 1부터 1씩 커지는 수를 말한단다.
그런데 우리는 이 세상의 모든 수를 자연수로만 표현할 수가 없었어.
예를 들면, 오늘 대구 아침 기온은 영하 5도 이고, 낮 기온은 영상 10도다라고 해보자.
우리는 수학하는 사람들이니깐, 영하 5도, 영상 10도를 하나의 수로 표현할 수 있어야 돼.
영하 5도는 -5, 영상 10도는 +10이라고 표현할 수 있겠다.
이렇게 해서 숫자 앞에 +[플러스], -[마이너스] 부호가 붙게 되면서, 정수라는 개념이 나오게 된 거야.
정수를 조금 더 자세하게 알아보자.
정수는 어떤 기준에 대해서 서로 반대가 되는 성질을 갖는 양을 수로 표현할 때, 한쪽을 +[플러스], 다른 한 쪽을 -[마이너스]를 붙여서 나타내는 것이거든. 말이 어려웠으니, 그림으로 예를 들어볼게.

이런 식으로 기준점이 정해져 있고, 반대되는 성질들이 있다. 그렇지? 그때, +, - 로 적절하게 표현할 수 있단다.
그리고 그 기준점을 0이라고 하는데, 이 수는 +, -가 아닌 중립적인 친구란다.
0 은 정말 중요한 수라서 더 자세하게 뒤에서 알려줄게.
그래서
자연수에 양의 부호 + [플러스]를 붙인 수를 양의 정수라고 한다. 예) +1, +2, +3 …
자연수에 음의 부호 - [마이너스]를 붙인 수를 음의 정수라고 한다. 예) -1, -2, -3 …
양의 정수, 0, 음의 정수를 통틀어 정수라 한다.
※ 양의 정수에서 양의 부호 +[플러스]는 생략이 가능하단다. 그리고 0은 양 그리고 음이 아닌 독보적인 친구란다.
| ⁕정리1) 1. 자연수는 1부터 1씩 커지는 수 2. 정수는 양의 정수, 0, 음의정수를 말한다. |
2. 유리수
정수에 이어서 새로운 수가 또 등장했어. 쌤이 설명하기 전에 유리수의 뜻을 먼저 말해줄게.
유리수란 분수로 나타낼 수 있는 수를 말하거든.
예를 들어서 설명해 줄게.

쌤이 적은 6개의 수가 보이니?
질문) 혹시 이 6개의 수를 분수로 표현할 수 있을까?
답변) 다른 수는 괜찮은데, 0을 잘 모르겠어요.
이 수들은 사실 분수로 다 표현이 가능하단다. 0 또한 분모가 0이 아닌, 분자가 0이라면 가능하지.

그래서 우리는 이 수들을 다 유리수라고 할 수 있겠다.
그러면 다른 질문
질문) 혹시 앞에 있는 수 3, 0, -7 은 어떤 수지?
답변) 자연수 모양에 플러스, 마이너스 붙인 것과, 0이 있으니 정수가 아닌가요?
정답! 이 세 수는 정수라고 배웠지? 그러면 옆에 있는 분수와 소수 모양으로 되어있는 이 세 수는 뭐라고 불러?
우리가 6개의 수가 다 유리수라 했는데, 3개는 정수이고 다른 애들도 이름을 지어줘야겠다!라고 해서 나온 것이 정수가 아닌 유리수란다.

이야.. 새로운 용어들이 왕창 나오기 시작했지?
그러면 혹시 유리수가 되지 않는 수는 어떤 수가 있을까?
그 수는 일단 중1 수준까지는 원주율 [3.141592…] 까지만 알면 될 것 같아. 원주율은 분수로 표현할 수 없어서 유리수가 되지 않는단다.
| ⁕정리2) 1. 유리수란 분수로 표현이 가능한 수를 말한다. 2. 정수가 아닌 유리수는 유리수에서 정수가 되지 않는 수를 말하는데, 쉽게 설명하면, 분수나 소수가 포함된다. |
3. 수직선 제대로 그리기
수직선은 초등학교 때부터 많이 들어 봤을 거야.
수+직선의 합성어인데, 직선을 쫘악! 그어두고 그 위에 수를 표현한 것이 수직선이란다.

초등학교 때까지는, 수직선을 1부터 했다면, 중학교 이후로는 중간을 0이라고 적고, 문제를 해결할 수 있도록 하자.
4. 양수와 음수 개념
중1에서 배우는 수의 개념 중 마지막이야. 많은 학생들이 가장 헷갈려하는 부분이거든.
이번 시간에는 양을 기준으로, 양수, 양의 유리수, 양의 정수는 확실하게 하고 갈게.
방금 3번에서 수직선 배웠으니깐, 한 번 써먹어보자.
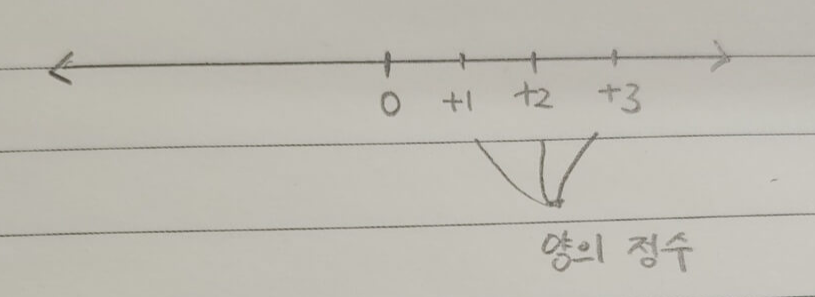
자 그러면 우리는 양의 정수를 표시할 수 있겠어? +1, +2, +3 이렇게 표시할 수 있겠다.
그러면 양의 유리수는? 유리수는 분수로 표현할 수 있는 수니깐, 몇 개만 찍어볼게.
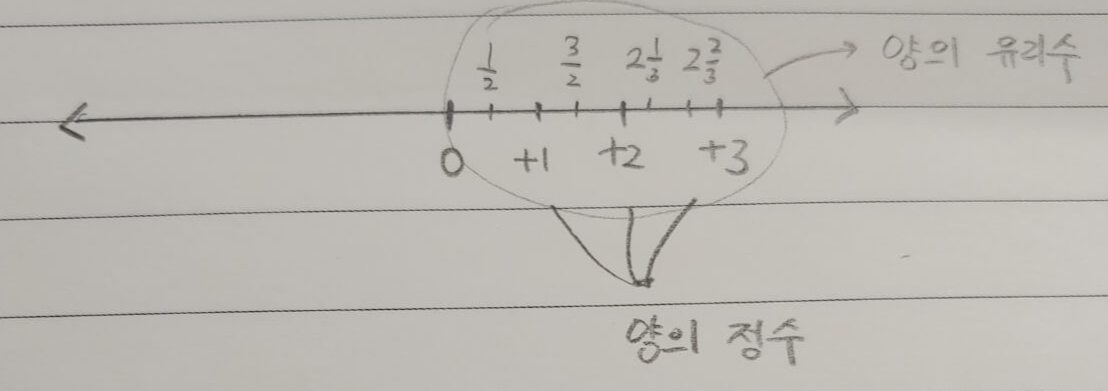
질문) 이 세상의 모든 유리수를 다 데리고 와서 수직선에 찍으면, 빈칸 없이 가득 찰까?
답변) 유리수를 다 찍긴 했지만, 방금 배웠던, 유리수가 되지 않는 원주율도 있지 않나요?
맞아. 아직 정확하게 알 필요가 없지만, 이 세상의 유리수로는 수직선을 다 표현할 수가 없단다. 나중에 중3에서 무리수라는 개념을 배우게 되니깐, 그때 자세히 알아보도록 볼게.
그러면 우리는 양수를 수직선에 표현해 볼 건데, 양수는 0보다 큰 수를 말하거든.
그럼 그 큰 수에는 양의 정수, 양의 유리수뿐 아니라 모든 양의 값들이 다 포함되니깐, 양수에는 원주율도 포함되어 있을 거야. 그래서 양수는 0보다만 크면 되는 수이지.

굳이 포함 관계로 표시하자면, 양의 정수 ⊂ 양의 유리수 ⊂ 양수 이렇게 표현할 수 있겠다.
[양의 정수 <<<< 넘사벽<<< 양의 유리수 <<<<<<<<넘사벽 <<<<<<<<<< 양수]
5. 중1 수의 체계 정리
많은 수들을 배웠으니, 정리가 필요해.
이 부분은 쌤이 그림으로 표현했으니, 확인해 봤으면 좋겠다.
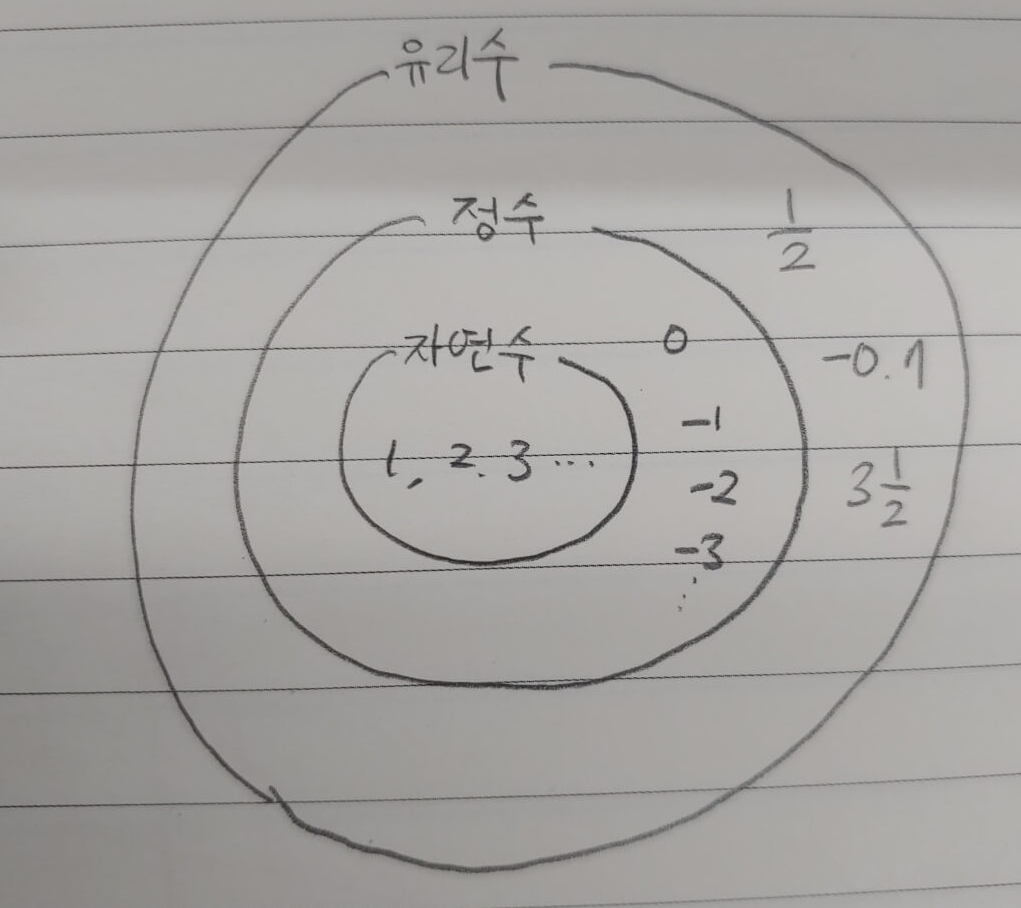
2단원 첫 시간인데, 새로운 용어들이 많이 나오게 되면서 공부할 분량이 많아졌을 것 같아. 쌤이 말해준 이 내용만 잘 정리해도 웬만한 문제는 충분히 다 풀 수 있을 거라고 믿고, 다음 시간에는 절댓값과 수의 대소 비교에 대해서 알아볼 거야.
- 끝 -
'수학 개념의 모든 것 > 중등수학' 카테고리의 다른 글
| [중1 기본] 3-1. 문자의 사용과 식의 값 완벽 마스터하기! (1) | 2023.01.27 |
|---|---|
| [중1 기본] 2-2 절댓값과 대소 관계 [부등호] 완벽 마스터하기! (0) | 2023.01.23 |
| [중1-1 기본] 1-7. 최소공배수 활용 완벽 마스터하기! (1) | 2023.01.21 |
| [중1-1 기본] 1-6. 최대공약수 활용 완벽마스터하기! (0) | 2023.01.19 |
| [중1 기본] 1-5. 공배수 최소공배수 완벽 마스터하기 (2) | 2023.01.18 |



